Une difficulté est couramment rencontrée : Comment s’assurer qu’une méthodologie d’étude est optimisée quant à son coût ?
Concrètement, il est parfois possible de diminuer la durée d’un questionnaire (sans pour autant dénaturer son contenu…) ou de réfléchir à un échantillonnage plus petit.
Le premier aspect pourra faire l’objet d’une future parution (car il y a beaucoup à dire), quant au second, il constitue le sujet qui nous intéresse aujourd’hui.
Cette lettre paraît conjointement à la mise en ligne sur notre site Internet heralis.fr, rubrique « Outils », de notre nouveau progiciel statistique vous aidant à constituer et à optimiser vos échantillonnages.
Vous êtes ainsi cordialement invités à vous rendre sur notre site et à nous poser des questions le cas échéant.
Pour constituer un échantillon, deux attitudes sont possibles : s’en remettre totalement à son Institut d’Études préféré ou se lancer seul dans l’exercice.
Dans les deux cas, il est bon de comprendre les incidences statistiques qu’engendre le choix d’interroger peu ou beaucoup d’individus pour réaliser son enquête.
Vous faire comprendre ces incidences, tel est l’objectif de cet article.
Comment choisir son échantillon ?
Comme nous venons de le rappeler dans notre préambule, budget et taille d’échantillon sont étroitement corrélés. Ainsi, dans une étude, le poste de dépense le plus élevé est fréquemment le terrain d’enquête.
Pour optimiser le coût d’une enquête, la première question à se poser est : « Est-il vraiment utile d’interroger autant d’individus ? ». Nous pourrions poser la question différemment, et se demander : « Une extrême précision dans mes résultats est-elle vraiment nécessaire face au budget engendré ? ».
En fait, tout le problème tourne autour de l’erreur statistique !
Mais qu’est-ce que « l’erreur statistique » ?
> C’est tout simplement l’écart entre :
• Ce que vous mesurez > Les résultats de votre sondage.
• Et la réalité > Si vous interrogiez l’ensemble de la population intéressée (par exemple tous vos clients).
Cet écart correspond à la précision statistique appelée aussi « Erreur d’estimation ».
Si nous regardons le graphe ci-dessous, il apparaît évident que la précision statistique peut coûter inutilement chère si on n’y prend pas garde.
Lien entre l’erreur d’estimation (ou précision statistique) et le nombre d’individus interrogés.
Que remarquons-nous ?
Pour passer de 6% à 4 % d’erreur (donc accroître de 2 points la précision statistique d’un sondage) notre échantillon doit s’accroître de 270 à 600 personnes.
>> L’erreur statistique c’est l’écart entre ce que vous mesurez et la réalité.
Au-delà de cette limite, pour gagner en précision, l’échantillon augmente très fortement (de manière exponentielle).
Ainsi pour se rapprocher d’une erreur d’estimation de 2% (contre 4% précédemment), ma population sondée devra s’élever jusqu’à 2 400 individus.
>> On dira que pour doubler la précision statistique, il faut multiplier par 4 la taille de l’échantillon.
Le choix d’un échantillon sera donc le fruit d’un arbitrage entre le coût du sondage (ou nombre d’individus interrogés) et la pertinence du choix de la précision statistique.
Tout va donc dépendre de la nature et des enjeux du sondage.
Pour éviter des déconvenues lors du lancement d’une étude, il semble nécessaire de maîtriser quelques notions statistiques.
Prenons un exemple : Sur 500 Parisiens interrogés, 47% sont satisfaits de la propreté des rues.
Par construction, dans notre exemple, nous dirons que 53% ne sont pas satisfaits.
Mes résultats sont-ils fiables ? En fait, si mon budget me donnait les moyens d’interroger l’ensemble des parisiens, obtiendrai-je les mêmes résultats ?
Pas sûr ! Ces pourcentages peuvent varier assez sensiblement et risquer d’inverser la tendance (les parisiens satisfaits seraient alors majoritaires).
Dans le jargon des statistiques, on dit que pour une population mère importante (ici, la population parisienne) et pour un échantillon de 500 personnes (notre exemple), l’erreur est de ± 4,4% pour un seuil de confiance à 95%.
>> Soyons plus explicite et reprenons terme à terme cette dernière proposition :
– La population mère : elle correspond à la population d’individus dans laquelle l’échantillon sera extrait.
Dans notre exemple la population mère correspond à la population parisienne. Par extension, cette population d’individus peut correspondre aussi bien à votre fichier clients ou même à un segment de votre fichier clients.
– L’erreur : elle correspond à l’écart d’estimation possible autour d’un pourcentage de répondants.
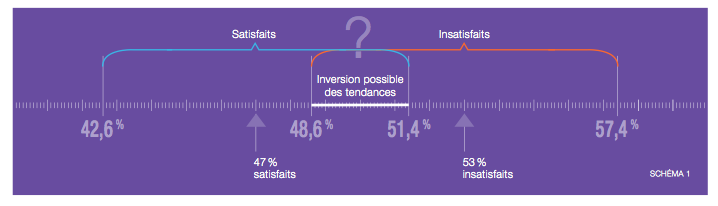
Dans notre exemple, nous avions 47% de « Satisfaits » et 53% « d’Insatisfaits ». Comme nous venons de le voir pour un échantillon de 500 individus, l’erreur est de ± 4%. On pourra par conséquent dire que les « Satisfaits » se situent entre 42,6 % et 51,4 % alors que les « Insatisfaits » se situent entre 48,6 % et 57,4%.
Le schéma ci-dessous illustre le chevauchement des deux intervalles. La zone de chevauchement délimite la zone de risque où l’inversion des tendances est possible, où les « Satisfaits » peuvent devenir majoritaires.
Ainsi, s’assurer de la qualité de son échantillonnage c’est aussi faire en sorte d’éliminer ce chevauchement.
Risque d’inversion des tendances : échantillon trop faible.
Mais, sommes-nous certain des ces intervalles ?
« Oui » mais à 95% (et non pas à 100%). C’est le seuil de confiance que nous définissons ci-dessous.
Le seuil de confiance (1) : dans les études de marché, on travaille généralement avec un seuil de confiance à 95%.
On dira alors que l’on a 95% de chance d’avoir un résultat qui se trouve effectivement (dans le cas des « Satisfaits ») entre 42,6% et 51,4%.
Dans les études de marché, on travaille généralement avec un seuil de confiance à 95%.
Par construction on pourra dire aussi que l’on a 5% de risque de se tromper (100% -95%) et de se retrouver en dehors de la fourchette d’estimation – Par exemple la réalité serait à 41% ou 52% pour les « Satisfaits ».
Notons que, si l’on souhaite diminuer la marge d’erreur (ou réduire la fourchette qui entoure notre pourcentage de 47% « satisfaits » ou 53% « d’insatisfaits »), c’est-à-dire aussi de réduire le risque de se retrouver avec une inversion des tendances (les satisfaits sont en fait majoritaires), il est alors nécessaire d’accroître l’échantillon.
(1) Remarque sur le seuil de confiance : Dans les sondages à caractère commercial on prend généralement 95% comme seuil de confiance. Pour passer à un seuil supérieur (99%), il faut alors augmenter la taille de l’échantillon. Le progiciel proposé sur heralis.fr permet d’échantillonner en choisissant le seuil de confiance.
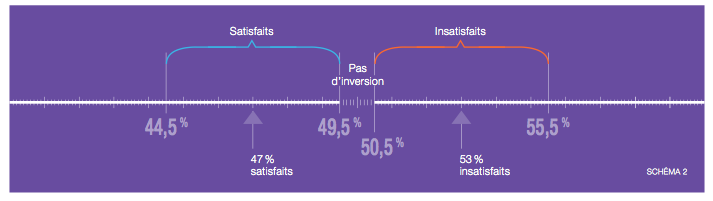
Ainsi, si nous augmentons l’échantillon pour atteindre 1 500 sondés, l’erreur est alors ramenée à ± 2,5%. Dans notre estimation, il n’y a plus maintenant de risque d’inversion des tendances.
Le schéma 2 illustre l’erreur ramenée à ± 2,5% autour des résultats de notre sondage.
Pour doubler la précision statistique il faut multiplier par 4 la taille de l’échantillon.
Accroissement de l’échantillon : l’inversion des tendances devient peu probable.
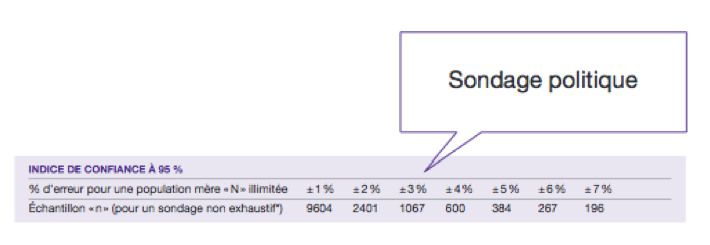
Le tableau qui suit donne la correspondance entre les pourcentages d’erreur et les échantillons interrogés pour une population mère très grande (on dit souvent illimitée, par exemple la population parisienne ou la population française). C’est le cas par exemple des sondages politiques.
Généralement, pour diminuer les risques d’inversion des résultats (dans notre exemple les satisfaits étant dans la réalité majoritaires), les sondages auprès d’une population de taille importante (et dont on présume des résultats proches de l’ordre de 50% de satisfaits et 50% d’insatisfaits), sont réalisés à partir d’échantillons d’au moins 1 000 personnes. Prenons l’exemple le plus connu, à savoir les sondages politiques qui sont pour la plupart réalisés auprès de 1 000 individus.
Cet échantillon correspond à un arbitrage coût du sondage sur précision statistique considéré comme correct pour ce type d’étude.
Dans les faits, l’actualité nous montre que le choix de retenir une erreur d’estimation fixée à 3,2% (c’est-à-dire à 1 000 individus sondés) nous place régulièrement dans la zone de chevauchement décrite au premier schéma, entraînant parfois des surprises aux élections… Pour bien faire, il serait nécessaire de sonder 10 000 futurs électeurs pour réduire l’erreur d’estimation à 1% (par exemple).
Quittons la politique et revenons au marketing.
Notons que travailler sur des échantillons issus de populations mères très grandes reste souvent théorique, car dans la réalité un responsable Marketing ne se situe que rarement dans le cas de figure des sondages politiques.
Ce dernier réalise des études à partir d’un fichier clients composé le plus souvent d’une population mère limitée.
Ainsi, deux notions sont à retenir : Quand une population mère est considérée comme illimitée (élections présidentielles par exemple), le sondage est dit « Non exhaustif ».
À l’inverse, quand la population mère est limitée (c’est souvent le cas en Marketing) le sondage peut s’avérer être « Exhaustif » sous certaines conditions que nous allons expliciter plus loin.
L’exhaustivité du sondage permettra alors de diminuer l’échantillonnage sans pour autant dégrader la précision statistique. La méthode est décrite dans la partie qui suit.
Optimisation de votre échantillon : Le cas du sondage exhaustif.
Soyons plus précis ! Un sondage est dit exhaustif quand le rapport : Échantillon choisi / population mère (noté n/N) est supérieur à 1/7 (ou 0,14 c’est-à-dire 14%). En d’autres termes, on considère en statistique que la proportion de 14% (1/7) pour un échantillon, représente une partie suffisante de la population mère pour parler de sondage exhaustif.
Reprenons notre exemple en nous limitant maintenant à la population de mon quartier. Ainsi, je souhaite maintenant réaliser un sondage, non plus auprès de l’ensemble des Parisiens, mais auprès des 2 500 habitants qui résident dans les rues aux alentours de mon adresse (et savoir s’ils sont satisfaits ou pas de la propreté des rues).
Alors que dans le premier cas, nous avions une population très importante considérée comme illimitée (environ 2 200 000 habitants pour Paris), nous avons maintenant une population plus restreinte évaluée à 2 500 habitants.
L’échantillon de 500 individus que nous avions choisi dans notre premier exemple est donc extrait maintenant d’une population mère 880 fois plus petite (2 500 x 880 = 2 200 000).
Et bien, les calculs statistiques doivent prendre en compte ces changements de proportion. Intuitivement cela peut aussi se comprendre !
>> Un peu de calcul :
Quand nous avions « n » notre échantillon de 500 individus pour une population mère « N » de 2 200 000 individus, notre rapport n/N (soit 500/2 200 000) était égal à 0,02 % donc inférieur à 14%.
Notre sondage n’était donc pas exhaustif.
Qu’en est-il de notre exemple ?
Notre échantillon « n » de 500 individus se rapporte maintenant à la population mère des 2 500 habitants de mon quartier. Le rapport n/N (soit 500/2 500) est alors égal à 20% (supérieur à 14%, condition de l’exhaustivité du sondage).
Notre échantillon de 500 personnes est alors considéré comme une part significative de notre nouvelle population mère.
Une optimisation de notre échantillon s’impose donc.
À précision statistique équivalente, des économies budgétaires sont par conséquent envisageables.
Comment déterminer l’échantillon optimisé : « n’ » ?
« n’ » est un ratio très simple qui prend en compte notre échantillon d’origine « n » et la population mère de mon quartier, à savoir : n’ = (n x N) / (n + N).
Remplaçons terme à terme les éléments du ratio par leurs valeurs respectives : Soit n’ = (500 x 2 500) / (500 + 2 500) = 1 250 000 / 3 000 = 416 individus.
Ainsi, interroger 416 individus auprès d’une population mère de 2 500 habitants donnera la même précision statistique (même erreur d’estimation) qu’en en interrogeant 500 pour une population mère très grande soit une économie budgétaire de 84 questionnaires.
>> Soulignons enfin ici que notre exemple illustre le cas général.
En aucune manière dans cet exemple nous prétendons expliciter l’ensemble des problématiques liées à la construction d’un échantillon.
En effet, certains aspects ne sont pas abordés ici.
Nous pensons notamment (sans pour autant être exhaustif), aux aspects liés à la construction du questionnaire (filtrage des questions diminuant le nombre de répondants) déterminants quant à l’échantillonnage à préconiser.
Les conseils de votre Institut d’Études restent donc toujours préférables !
Pour vous permettre d’estimer vous-même vos échantillons (et, nous l’espérons, à la lumière de ces explications), HERALIS a mis en place un progiciel sur son site www. heralis.fr rubrique « Outils » – Échantillonnage.
D’autres outils sont à votre disposition sur heralis.fr : Test de tendance et Test comparaison de deux moyennes.
Annexe pour les « férus » de statistiques
n = Échantillon
e = erreur
P = Proportion observée dans l’échantillon*.
• n = (P x 1-P) / (e/1,96)2
*la valeur 1,96 est relative à la lecture de la table de Student.
Pour plus de précision Cf. les manuels de statistiques.
Simplifions et posons :
P=0,5 (Cf. P ci-dessous) et 1,962 = 3,84 (arrondissons à 4)
Alors n = 1/e2
Reprenons notre exemple :
Pour notre erreur de ± 4% on a bien 1/(0,044)2 = 516 (environ 500)
Notons ici que « n » ne doit pas être inférieur à 30 individus. Si c’est le cas, faites un recensement.
• e = [P-1,96 x (P x (1-P)/n) ; P+1,96 x (P x (1-P)/n)]
En remplaçant P par 0,5 on obtient
e = ± 1/ (n) soit e = ± 1/ 500 = ± 4,4%
* Par défaut P est généralement fixé à 0,5 (ou 50%). C’est en fait la situation la plus défavorable que nous retenons habituellement, celle qui donne l’intervalle de confiance le plus large.
Prenons un exemple : À la question : « Êtes-vous joueur de tennis ? » Oui / Non.
Après une première enquête dite pilote, ou après s’être documenté on peut présumer des proportions (par exemple Oui : 30% / Non : 70%).
Dans ce cas P = 30% (donc 1-P=70%). Mais il n’est pas toujours simple de connaitre P a priori.
Attention ! Soulignons ici (comme le montre la formule de « n ») que le choix des proportions a une incidence sur la taille de l’échantillon.
Dans le doute conservez le cas général P = 0,5.
Pierre MOLINA
La lettre HERALIS : Échantillonnage et précision statistique – Comment optimiser vos échantillons >
http://www.heralis.com/newsletters.php?fid=bmV3c2xldHRlcnMvNzAucGRm&readers=0
Outils statistiques / Outils d’échantillonnage >
http://www.heralis.com/site/index.php?option=com_content&view=article&id=60&Itemid=78
>> SatiCommerce : Enquêtes et questionnaires de satisfaction en ligne.
Créez votre enquête et votre questionnaire de satisfaction : hôtels, campings, restaurants, commerçants, réseaux de points de vente, marques franchisées …
A lire aussi :
- Avec SatiCommerce, finis les questionnaires papier !
- Avec SatiCommerce, participez à votre e-Réputation.
- Avec SatiCommerce, recueillez les vrais avis de vos clients.
- Des statistiques de mesure de la satisfaction clientèle simples et efficaces.